Distribución bidimensional, distribución estadística en la que intervienen dos variables, x e y, y, por tanto, a cada individuo le corresponden dos valores, xi, yi. Estos dos valores se pueden considerar como coordenadas de un punto (xi, yi) representado en un diagrama cartesiano. Así, a cada individuo de la distribución le corresponderá un punto, y toda la distribución se verá representada mediante un conjunto de puntos.
Por ejemplo, supongamos que si a los cinco hijos, A, B, C, D y E, de una familia se les pasan unas pruebas que miden la aptitud musical (Mu) y la aptitud para las matemáticas (Ma), se obtienen los siguientes resultados:

Esta tabla es una distribución bidimensional porque intervienen dos variables: valoración Mu, valoración Ma. A cada individuo le corresponden dos valores: A(5,6), B(7,10), C(4,5), D(8,6), E(2,4). De este modo se asocia a cada individuo un punto en un diagrama cartesiano:

CORREALCION:
Esta representación gráfica de una distribución bidimensional se llama nube de puntos o diagr Correlación, en estadística, relación entre las dos variables de una distribución bidimensional. Se mide mediante el coeficiente de correlación, r.
Si los datos de la distribución son (x1,y1), (x2,y2),…, (xn,yn), el coeficiente de correlación se obtiene mediante la fórmula:
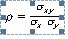
en donde σxy es la covarianza, y σ x, σ y son las desviaciones típicas de las dos variables.
El valor del coeficiente de correlación oscila entre –1 y 1 (-1 ≤ r ≤ 1). En cada caso concreto, el valor de r indica el tipo de relación entre las variables x e y.
Cuando |r|es próximo a 1, la correlación es fuerte, lo que significa que las variaciones de una de las variables repercuten fuertemente en la otra. Mientras que si |r|es próximo a 0, la correlación es muy débil y las variables están muy poco relacionadas.ama de dispersión.
Entre las dos variables que determinan una distribución bidimensional puede existir una relación más o menos estrecha que se llama correlación, y se puede medir mediante el coeficiente de correlación, r, que es un número, asociado a los valores de las dos variables. El coeficiente de correlación puede valer entre -1 y 1.
Cuando r = 1 existe una relación funcional entre las dos variables de modo que el valor de cada variable se puede obtener a partir de la otra. Los puntos de la nube están todos situados sobre una recta de pendiente positiva.

Esto ocurre, por ejemplo, cuando una barra metálica se somete a distintas temperaturas, x1, x2,…, xn, y se miden con precisión sus correspondientes longitudes, y1, y2,…, yn. Las longitudes se obtienen funcionalmente a partir de las temperaturas de modo que, conociendo la temperatura a que se va a calentar, se podría obtener la longitud que tendría la barra.
Cuando r es positivo y grande (próximo a 1) se dice que hay una correlación fuerte y positiva. Los valores de cada variable tienden a aumentar cuando aumentan los de la otra. Los puntos de la nube se sitúan próximos a una recta de pendiente positiva.

Es el caso de las estaturas, x1, x2,…, xn, y los pesos, y1,y2,…, yn, de diversos atletas de una misma especialidad. A mayor estatura cabe esperar que tengan mayor peso, pero puede haber excepciones.
Cuando r es próximo a cero (por ejemplo, r = -0,12 o r = 0,08) se dice que la correlación es muy débil (prácticamente no hay correlación). La nube de puntos es amorfa.

Es lo que ocurriría si lanzáramos simultáneamente dos dados y anotáramos sus resultados: puntuación del dado rojo, xi; puntuación del dado verde, yi. No existe ninguna relación entre las puntuaciones de los dados en las diversas tiradas.
Cuando r es próximo a -1 (por ejemplo, r = -0,93) se dice que hay una correlación fuerte y negativa. Los valores de cada variable tienden a disminuir cuando aumentan los de la otra. Los puntos de la nube están próximos a una recta de pendiente negativa.

Si en un conjunto de países en vías de desarrollo se miden sus rentas per cápita, xi, y sus índices de natalidad, yi, se obtiene una distribución de este tipo, pues suele ocurrir que, grosso modo, cuanto mayor sea la renta per cápita menor será el índice de natalidad.
Cuando r = -1 todos los puntos de la recta están sobre una recta de pendiente negativa. Existe una relación funcional entre las dos variables.

COMENTARIO

No hay comentarios:
Publicar un comentario